Pour certains développements on a besoin de générateur de nombres aléatoires. Attention ! on est bien d’accord que tous ne se valent et qu’en particulier les morceaux de code proposés ici ne permettent en aucun cas de sécuriser des échanges. Au contraire, les algorithmes présentés ici ont une faible qualité au profit de bonnes performances calculatoires et d’une faible empreinte mémoire ; ils sont par exemple extrêmement prévisibles puisque chaque valeur est calculée à partir d’un état précédent.
Quand cela est possible, il faut utiliser les bibliothèques disponibles qui seront toujours de meilleure qualité que le code écrit par un développeur seul.
Générateur Congruentiel Linéaire (Wikipédia)
Parmi les générateurs, il existe une famille basée sur des calculs simples comme une addition, une multiplication avec une constante et un modulo (reste de la division entière). Cette famille s’appuie sur la formule générale suivante :
Xn+1 = (a * Xn + c) mod m
Toute la difficulté consiste évidemment dans le choix de ces constantes afin que le générateur ait une période la plus longue possible (avant de générer les mêmes nombres) et la meilleure distribution possible des valeurs (répartition).
Il existe un sous-groupe de ces générateurs dit Lehmer ou encore Park-Miller, pour lequel la constante c est nulle (ce qui évite l’addition) mais aussi d’autres propriétés de m (premier ou puissance d’un nombre premier) et de rapport entre a et m. (WP). On pourra retenir la version appelée « MINSTD » (standard minimal) qui retient les constantes suivantes :
m = 2³¹ - 1 ; a = 48271 ; c = 0
C’est un générateur de nombre de 32 bits, sans addition donc, mais qui nécessite d’utiliser une multiplication d’un entier de 64 bits avec la constante de 16 bits pour son calcul :
uint32_t lcg_parkmiller(uint32_t *state) {
return *state = ((uint64_t)*state * 48271u) % 0x7fffffff;
}
/// @source https://en.wikipedia.org/wiki/Lehmer_random_number_generator#Sample_C99_codeIl existe une implémentation plus longue qui permet de ne manipuler que des entiers de 32 bits. L’algorithme mixe à la fois le modulo (reste de la division) et la multiplication :
uint32_t lcg_parkmiller(uint32_t *state) {
const uint32_t N = 0x7fffffff;
const uint32_t G = 48271u;
const uint32_t div = *state / (N / G);
const uint32_t rem = *state % (N / G);
const uint32_t a = rem * G;
const uint32_t b = div * (N % G);
return *state = (a > b) ? (a - b) : (a + (N - b));
}
/// @source https://en.wikipedia.org/wiki/Lehmer_random_number_generator#Sample_C99_codeXorShift (Wikipédia)
Il s’agit de générateurs basés sur des opérations arithmétiques de base que sont les décalages (multiplication et division par une puissance de 2) et les OU-Exclusifs (XOR) qui sont souvent réalisées atomiquement par les processeurs. Ils ont le grand avantage de ne pas faire appel à la multiplication ou au reste de la division qui sont de grands consommateur de temps CPU. À nouveau, ces générateurs ne sont pas destinés à des application de sécurité ou de cryptographie.
Suivant les longueur de la séquence de nombre à produire, on utilisera des entiers plus ou moins grands.
Pour des processeurs de faible puissance, on pourra utiliser des entiers de plus petite taille, comme ici une implémentation en entiers de 16 bits et une période de seulement 216 – 1 = 65’535 (http://www.retroprogramming.com/2017/07/xorshift-pseudorandom-numbers-in-z80.html) :
uint16_t xorshift16( ) {
// Plusieurs jeux de décalages sont utilisables :
// [6, 7, 13], [7, 9, 8], [7, 9, 13], [9, 7, 13].
static uint16_t x = 1;
x ^= x << 7;
x ^= x >> 9;
return ( x ^= x << 8 );
}George Marsaglia de l’Université de l’État de Floride a publié son travail dans ce document (https://www.researchgate.net/publication/5142825_Xorshift_RNGs) où il présente des implémentations de référence avec des entiers de 32 et 64 bits.
Voici celle avec des entiers de 32 bits et une relativement faible période de 232 – 1 (> 4,29.109) :
uint32_t xorshift32() {
static uint32_t x = 2463534242;
x ^= x << 13;
x ^= x >> 17;
return ( x ^= x << 5 );
}Et celle avec des entiers de 64 bits et une période de 264 – 1 (> 1,8 . 1019) :
uint64_t xorshift64() {
static uint64_t x = 1;
x ^= x << 13;
x ^= x >> 7;
return ( x ^= x << 17 );
}Il serait possible de continuer avec des entiers plus grands encore, 64 bits par exemple, mais une autre technique existe aussi qui consiste à garder des entiers limités, mais a augmenter la période en utilisant plusieurs entiers pour former des n-uplets (doublets, triplets, quadruplets…). Ces entiers permettent de conserver en mémoire les tirages précédents pour s’en servir dans le calcul du prochain résultat.
Ce court article donne une version 8 bits du xor128, ci-dessous (http://www.donnelly-house.net/programming/cdp1802/8bitPRNGtest.html). Jusqu’ici mes tests donnent une période de plus de 1 milliard.
uint8_t xor32??() {
static uint8_t x = 21, y = 229, z = 181, w = 51;
const uint8_t t = (x ˆ (x << 3));
x = y;
y = z;
z = w;
return ( w = (w ˆ (w >> 5)) ˆ (t ˆ (t >> 2)) );
}Pour une période de 264 – 1 (> 1,8 . 1019) et en produisant des nombres de 32 bits seulement, on aura le code :
uint32_t xor64() {
// Coef possibles [10, 13, 10], [8, 9, 22], [2, 7, 3], [23, 3, 24]
const byte a = 10, b = 13, c = 10;
static uint32_t x = 1234, y = 5678; // pas tous nuls
const uint32_t t = (x ˆ (x << a));
x = y;
return ( y = (y ˆ (y >> c)) ˆ (t ˆ (t >> b)) );
}Une implémentation de référence est donnée pour une période de
2128 – 1 (> 3,4 . 1038 : ça fait plus que d’étoiles dans l’univers) avec un quadruplet :
uint32_t xor128() {
static uint32_t x = 123456789, y = 362436069, z = 521288629, w = 88675123;
const uint32_t t = x ˆ (x << 11);
x = y;
y = z;
z = w;
return ( w = (w ˆ (w >> 19)) ˆ (t ˆ (t >> 8)) );
}Avec cette famille de générateurs de nombres pseudo-aléatoires, on reste sur des série en loi uniforme (la probabilité d’apparition d’une valeur entière est constante quelle que soit la valeur attendue, sur intervalle), qu’il faudra adapter selon les besoins finaux.
Je n’ai retenu que ces deux familles de générateurs mais il en existe beaucoup d’autres qui apportent plus de qualité mais qui nécessitent aussi plus de puissance de calcul.
Distribution normale
Les générateurs vus précédemment ont une distribution uniforme des nombres générés (chaque valeur entière à la même probabilité d’apparaitre dans une séquence d’une longueur donnée).
Mais parfois on préfèrera une distribution « normale » des nombres, c’est à dire dont la probabilité croit, puis décroit de part et d’autre d’une valeur centrale suivant la fameuse gaussienne.
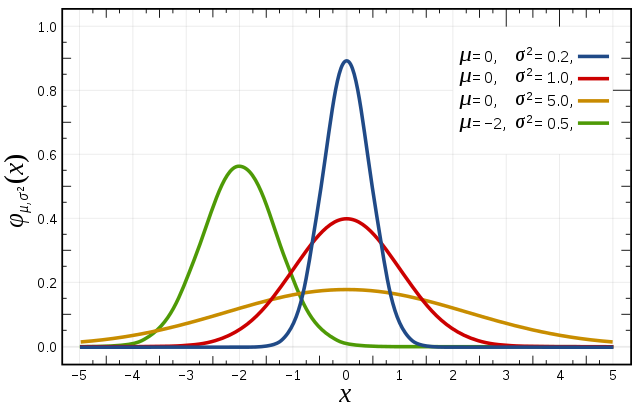
Il existe là aussi plusieurs méthodes pour transformer une distribution uniforme en distribution normale, suivant la précision attendue et la complexité des calculs.
Méthode de Box-Muller (Wikipédia)
Cette méthode utilise deux tirages successifs à distribution uniforme pour générer un tirage à distribution normale. Elle utilise massivement des calculs à virgule flottante (double) avec le cosinus, le logarithme et la racine carrée, ce qui peut la rendre très lente.
Avec une fonction rand() qui retourne une valeur entière entre [0,RAND_MAX], on pourra écrire :
#define RAND ((double) rand())/((double) RAND_MAX)
double NormalDistribution(double mu, double sigma) {
const double TWOPI = 2.0*3.141592653589793238462643383279502884197169399375;
return (mu + sigma * sqrt(-2.0 * log(RAND)) * cos(TWOPI * RAND) );
}
// @source https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Box-MullerThéorème Central Limite (Wikipédia)
« Ce théorème […] établit la convergence […] de la somme d’une suite de variables aléatoires vers la loi normale. Intuitivement, ce résultat affirme que toute somme de variables aléatoires indépendantes tend dans certains cas vers une variable aléatoire gaussienne. » — Wikipédia.
L’application simple de ce théorème est que la somme de suffisamment de tirages à distribution uniforme produit une distribution normale. En fait, dès 12 répétitions, on obtient une distribution « utilisable », certains indiquent que 6 suffisent. Comme précédemment, avec une fonction rand() qui retourne une valeur entière entre [0,RAND_MAX], on pourra, cette fois, écrire :
#define RAND ((double) rand())/((double) RAND_MAX)
double NormalDistribution(double mu, double sigma) {
const byte NB = 12;
long unsigned somme = 0;
for (byte i = 0; i < NB; ++i) {
somme += rand();
}
return (mu + sigma * ( ((double)somme) / ((double) RAND_MAX) - NB / 2.0d) );
}Et là, le code est beaucoup plus simple et rapide (malgré la boucle) et n’utilise pas de fonctions transcendantes, très couteuses en temps de calcul sur un « petit » processeur.
